【摘要】在三维建模过程中，覆盖层地质体由于其形态的复杂，其下底面的建模往往费时且效果不佳。通过研究覆盖层的成因和发育特征，可将其划分风化残积型与侵蚀堆积型两类，按数据处理流程可分别对应厚度控制型与高程控制型。本文探索了狄洛尼三角插值法、反距离加权法以及线性插值法在上述两类覆盖层建模中的组合应用，并通过不断优化，极大提高了建模效率。通过某水电站几种不同成因覆盖层的实际建模应用，表明该建模方法较为理想，可供工程技术人员参考并推广应用。

【关键字】覆盖层；下底面三维建模；算法

1 研究背景

随着BIM技术的推广应用，工程技术人员对于创建地质体三维模型的效率与精度的要求日益提高[1]。在覆盖层地质体的创建过程中，技术人员习惯于将其上表面向下偏移一个固定厚度，然后对其进行形态变形以通过已知点的方法来建立。但由于地表覆盖层形态的复杂、厚度的分布不均，该方法无法正确反映覆盖层发育的真实规律；且由于变形算法本身的不可控，其生成的下底面往往差强人意、精度较低；如果通过人工修改则极为费时，且效果不佳，无法进行动态更新。针对以上操作方法的严重不足，本次研究探索了不同覆盖层成因下下底面的插值方法，提高了地质体建模的效率与精度。

2 建模方法研究

2.1建模思路

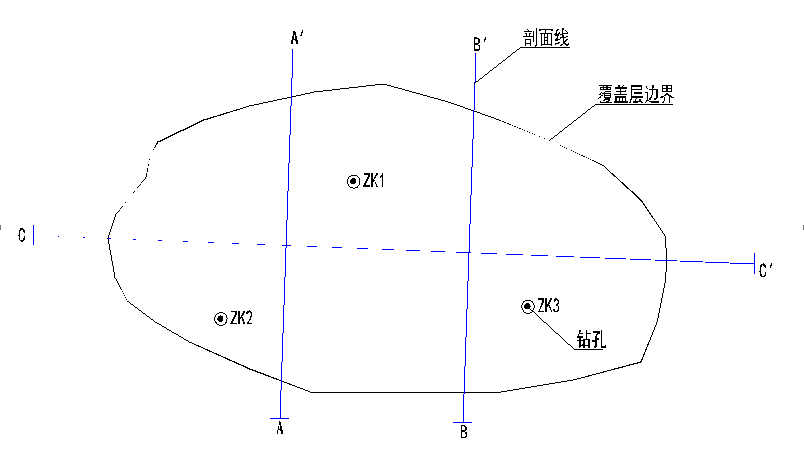
图1 覆盖层边界与已知元素的关系

在岩土工程勘察中，可以获得与覆盖层有关的数据有：覆盖层上表面、边界（含地质点）、钻孔数据（覆盖层厚度）和剖面图，其相互关系如图1所示。其中边界处覆盖层厚度为0m，钻孔处厚度已知，剖面线可以通过取样转换为点（如图2）。以上点的高程和厚度均已知，统称为已知点。相对于整个覆盖层范围而言，已知点的数量往往相当有限，需要编写插值算法对已知点之间的未知区域进行合理的推测计算，以获得连续完整的区域性数据，从而通过曲面转换获得覆盖层下底面模型。该建模的核心在于根据已知点对未知区域进行插值，因此可靠、快速的插值算法是下底面模型建立的关键。

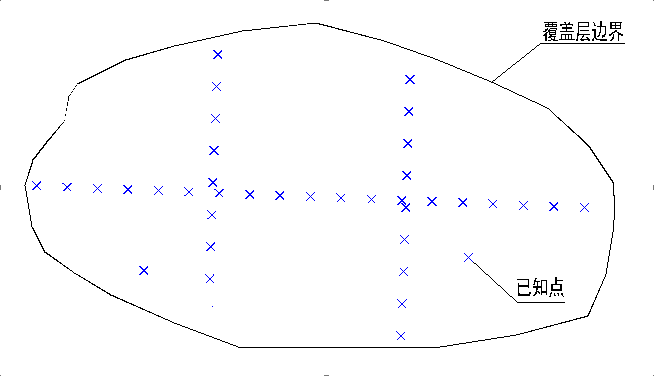
图2  剖面图与钻孔数据均转换为已知点

2.2 覆盖层厚度变化规律分析与插值算法选择

自然成因的覆盖层常见的形式有残积、坡积、冲积、洪积、滑坡堆积等，不同成因的覆盖层按其厚度与地形的相互关系可以划分为风化残积型与侵蚀堆积型两类。

对于风化残积型覆盖层，岩石风化与原岩抗风化特性、区域地壳运动及气候条件等有关，其厚度受地面地形的影响较大，与地形坡度有较大联系。一般地形平缓处较厚，斜坡处较薄，当坡度＞45°时一般极薄，陡坡处厚度几乎为0m。因而其下底面一般随地表地形的起伏而波动。当存在已知点时，其厚度控制范围一般为30-50m，局部可能会存在突变，距离越近影响越明显，但同一方向上只受到最近已知点的直接影响。如图3，在同一方向上点3处的厚度只受点1的影响，点2的影响可以忽略。该类型覆盖层可以概括为厚度控制型。

对于侵蚀堆积型覆盖层，其厚度与地面地形的关联较少，一般较为稳定。其下底面平整连续，呈水平或缓倾状，表现为侵蚀停止时的原始特征。其厚度仅在沟槽处出现条状变薄，在前缘处随地形变薄，在后缘处自然尖灭。该类型覆盖层可以概括为下底面高程控制型。

上述两类覆盖层共有的变化规律为：1）边缘处厚度为0m；2）从边缘往中部逐渐变厚，但存在随机性。 

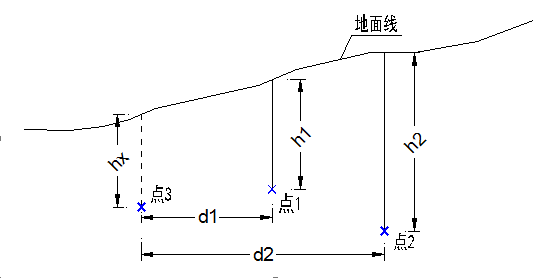
图3 同一方向上不同点对插值点的影响

针对覆盖层厚度分布的上述特点，在进行插值算法选择时应满足以下要求：1）覆盖层边缘处厚度值应为0m；2）已知点处厚度值应保持不变；3）与已知点距离越近，受其影响越大，且同一方向上应只考虑最近点的直接影响；4）插值应连续、较光滑，不能出现随机性陡坎；5）新增、删除、修改已知点时仅对修改点附近区域的计算产生影响，从而保证算法的稳定性；6）算法应简洁实用，利于在工程技术人员中推广使用。对此，可将需插值的区域划分为3部分：①为已知点控制的区域；②为边界附近渐变的区域；③为①与②之间的过渡区域，见图4。

针对上述要求，对三维建模中曲面插值常用的算法进行了对比研究，如反距离加权法、线性插值法、最小曲率插值法、多元回归插值法、样条函数插值法、克里金法（Kriging）[2]、狄洛尼三角插值法等，以针对不同的区域选择相应的算法[3]。

对于厚度型覆盖层，其插值对象是厚度值。考虑到算法的简洁、高效，本研究针对核心部分（区域①）选择了狄洛尼三角插值法，该方法在计算时选择不在同一方向的对插值点影响最大的3个已知点进行插值计算，符合覆盖层发育的一般规律；对边界附近（区域②），覆盖层一般沿地表地形自然尖灭，可以采用线性插值法；对边界与已知点之间（区域③），为了保证插值数值的连续、光滑，则采用反距离加权法过渡。通过以上3种算法的组合运用，能很好是满足覆盖层插值计算中的上述需求。获得厚度值后，可以通过原地面高程与插值计算得到的厚度相减，即可得到所需下底面高程值 [4][5]。

对于下底面高程控制型覆盖层，其插值对象是高程值，区域①、②、③合并为一个区域，直接采用狄洛尼三角插值法，计算结果即为覆盖层下底面高程值。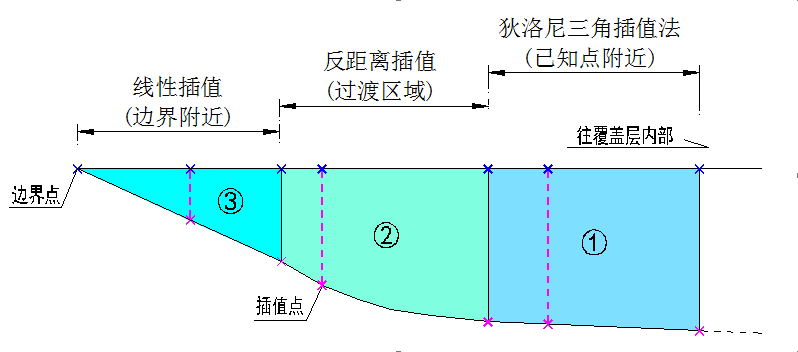 

图4 插值区域的划分及算法的选择

3 插值算法的实现

厚度型插值计算需首先获得已知点处的厚度值，数据处理流程见图5（a）;高程插值计算数据处理流程见图5（b）。

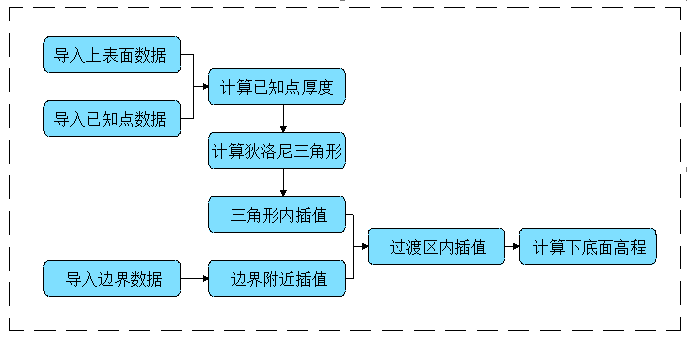
a. 厚度插值计算

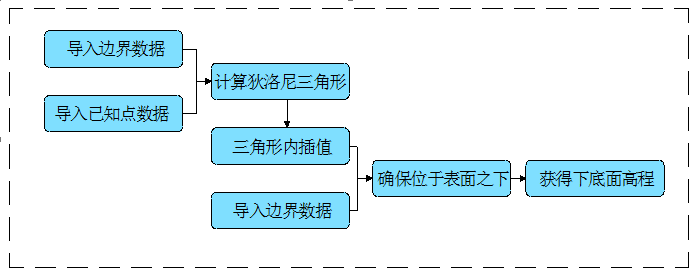
b. 高程插值计算

图5 插值计算数据处理流程图

3.1 狄洛尼三角插值法插值

3.1.1 狄洛尼三角剖分的原理

给定平面上的一组点，将平面细分成以这些点为顶点的多个三角形，该三角形满足条件：

（1）任意一个三角形除了端点外，不包含其它任何点。

（2）三角形的边互不相交。

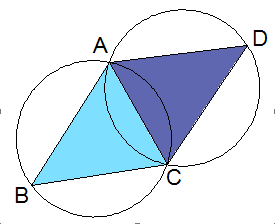
图6 狄洛尼三角形的生成

3.1.2 剖分后三角形的特点

（1）最接近：以最接近的三点形成三角形。

（2）最大化最小角特性：在可能形成的三角剖分中，狄洛尼三角剖分所形成的三角形的最小角最大。从这个意义上讲，狄洛尼三角网是“最接近于规则化的”三角网（在两个相邻的三角形构成凸四边形的对角线，在相互交换后，两个内角的最小角不再增大）。

（2）唯一性：不论从区域何处开始构建，最终都将得到一致的结果。

（3）区域性：新增、删除、移动某一个顶点只会影响邻近的三角形。

从以上特点可以看出，其剖分后的三角形完全满足2.2节中插值时对已知点的选择要求，同时形成的三角网最小角最大，既能保证采用的已知点能在插值点周围最大均匀化分布，亦能优先利用对插值点影响最大的三个已知点。且该算法具有计算唯一性、稳定性好的优点。

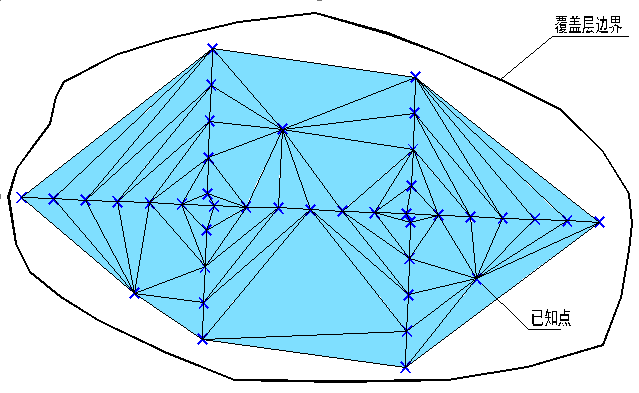
图7 典型覆盖层进行狄洛尼三角剖分后的效果

3.1.3 三角剖分后三角形内插值

三角剖分完成后，即可对每个三角形网格内的值进行插值计算。选择插值算法时，要考虑到以下几点：（1）在3个已知点处的值应保持不变；（2）边界处与边界以外的值应保持连续性；（3）算法的简便性。对于已知点较多，且对精度要求不高时，可以选择简单实用的平面插值法，即直接计算出空间中通过3个已知点构成的平面，再通过插值点的平面位置即可计算出该该点的厚度值或高程值。该算法除满足以上3点要求外，计算出厚度后还能在计算高程时保证原始地面地形变化对下底面的影响，与实际地质情况非常接近。

3.2 边界处线性插值法插值

覆盖层的厚度往往会从边界处的0m往内部逐渐过渡，到一定距离处则不再受边界的影响，不同的岩层和区域影响范围各不相同，在缺少实测资料时该距离可取已知厚度最大值的一倍左右。在该范围内，直接采用线性插值的算法。

3.3 过渡区反距离加权法插值

对于三角形以外的插值点，当其与边界超过一定距离时，受边界的影响很小，可以全部利用已知点进行插值。选择插值算法时，需要考虑到以下几点：（1）距离已知点较近时应受已知点的影响；（2）各拟插值点与周围已插值点的值应保持连续性；（3）当离已知点较远时，可以综合考虑所有已知点的平均趋势。针对以上特点，本研究选择了通用的反距离加权法，该算法在距离已知点较近时，能与已知点保持较好的连续性，当距离逐渐变远时，则反映了整个区域所有已知点的平均厚度趋势，对于地质工作者来说，在勘探资料有限时，这也是能暂时接受的成果。

3.4 下底面三角网模型的建立

插值计算完成后，即可得到下底面高程点数据，通过点云处理，即可生成三角网并转化为曲面模型。

3.5 局部优化

对于三角形外离已知点较远的区域，其获得的高程值可以根据覆盖层在不同地貌处发育的特点进行平顺和优化。在山包处，覆盖层往往更厚，在冲沟处，则会变薄，总体表现为更平顺，见图8。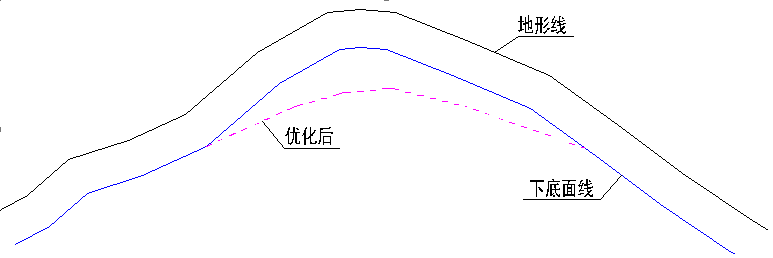 

图8 山包处覆盖层下底面的平顺与优化

4 建模效果分析与迭代改进

4.1 建模效果分析

通过运用以上建模方法开发出计算机程序，在以上步骤完成后，对得到的下底面模型进行检查可见：（1）边界与已知点处均能与给定值保持吻合；（2）其余部分插值点均位于上表面之下，不需要人工处理；（3）得到的模型整体平顺，连接自然，符合覆盖层的发育规律；（4）算法高效简洁，对于面积为40万平方米的覆盖层计算时间在1分钟左右，能满足实际需求。

4.2 模型的迭代改进

在实际应用中，在已知点缺乏的区域，当计算成果与地质工程师的判断有出入时，可以在该部位添加虚拟剖面，将工程师的认识通过该剖面表达出来，并转化为点后添加到原数据中重新计算。通过以上步骤的迭代使用，不断优化下底面曲面，最终可获得较为理想的覆盖层地质体模型。

5 建模实例

对某水电站坝址区覆盖层进行了建模测试，生成的覆盖层地质体见图9，校核剖面图见图10。该坝址共分布有5处不同类型覆盖层，其中①和⑤为阶地堆积层，属于侵蚀堆积型；②为滑坡堆积层，属于风化残积型；③、④以残积堆积层为主，属于风化残积型。从图中可以看到，所有覆盖层模型边界清晰、层次分明，下底面连续完整，其形态符合地层发育的一般规律。实践表明该方法能较好地适用于地质体的建模。

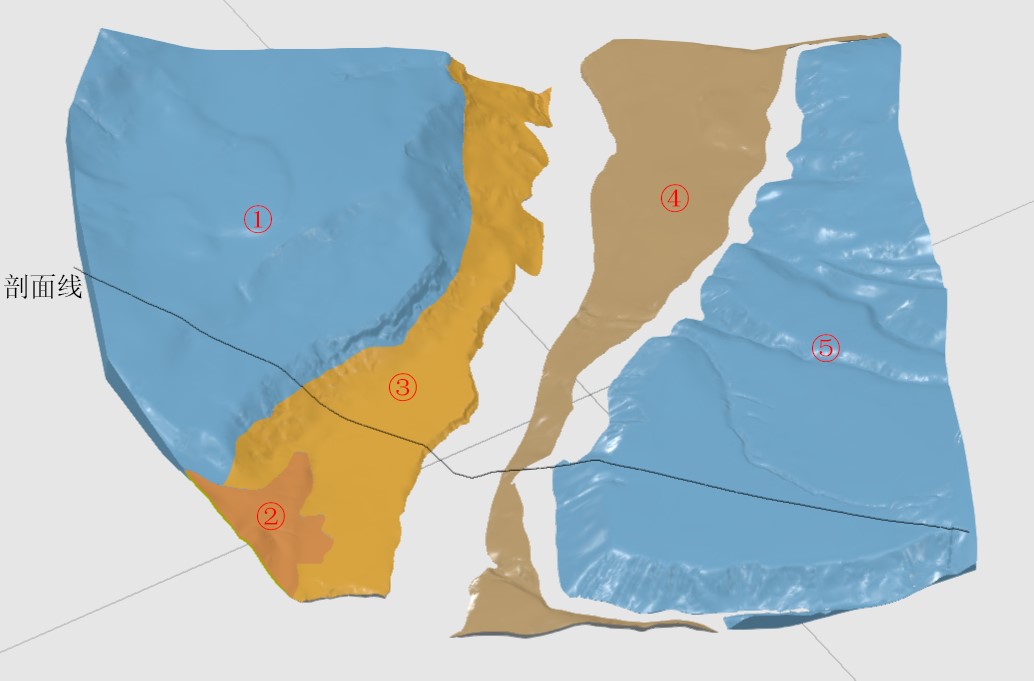
图 9 某水电站坝址区覆盖层建模效果（空白处为基岩）

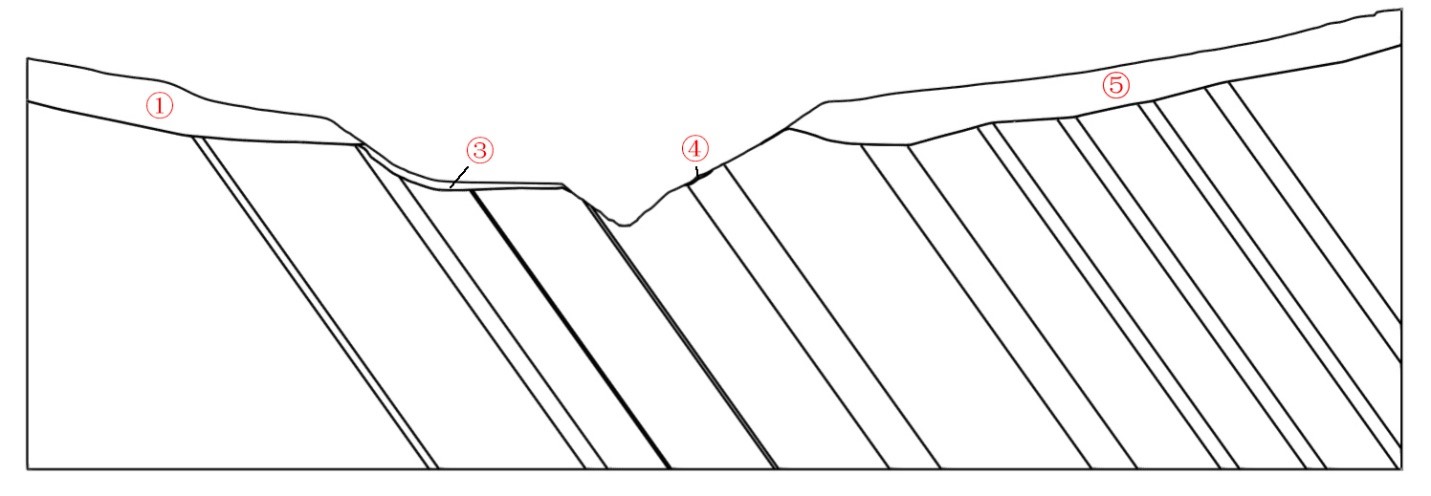
图10 某水电站坝址区覆盖层建模后剖面检查效果

6 结语

文中详细介绍了覆盖层下底面三维建模计算的一种全新方法的理论与实践。该方法通过对覆盖层分布规律与已知条件的分析，将覆盖层划分为风化残积型与侵蚀堆积型两类，通过研究选择了与之相适应的插值计算方法，在经过优化和迭代改进后，最终能获得效果极佳的下底面模型。该方法高效简洁，边界条件容易获得，程序易于实现，且对提高建模速度及提升模型质量效果显著。相信通过持续改进后，可以为覆盖层的三维地质建模带来本质的飞跃。

参考文献

[1]姬广军等，三维地质建模技术研究现状，工程技术，2019年4月；

[2]胡瑞华等，复杂基岩覆盖层分界面建模算法研究和实现，人民长江，第49卷第15期；

[3]赵意等，三维地质建模在水利工程勘察中的应用，资源信息与工程，第34卷第2期；

[4]高军等，郑万高铁不良地质三维建模与修正分析，隧道建设（中英文），第38卷增刊2；

[5]刘珊珊，理正勘察三维地质软件对工程地质三维建模的实现，工程技术，2018年11月中。

作者简介

张必勇，男，高级工程师，主要从事水利水电工程地质勘察等方面的工作，参加或主持完成了缅甸密松水电站各阶段工程地质勘察工作、巴基斯坦Karot水电站各阶段工程地质勘察工作，以及多个堤防、水库的工程地质勘察工作。

E-mail: 33022866@qq.com，电话：13971619100